Understand the physics & math.
The math is pretty simple, its just a transformer.
The trick though, is to stay within certain operating parameters and limitations.
Lets deal with the very easy ones first to get them out of the way.
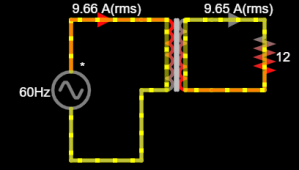
The current rating has nothing to do with the core, only temperature rise in the secondary winding.
The flux swing in the core depends upon the turns, the frequency, and the cross sectional area (Faraday's Law)
And of course the turns ratio. All this is no different to designing an ordinary garden variety voltage/power transformer.
Now the tricky bits.
We want it to be small, because its not transferring much power. But a small core cross sectional area, requires a lot of turns, especially at very low frequencies. So we arrange things so it has say 1,000 turns and saturates at a few volts with that combination of turns and core cross section.
Now we want the inductance to be high enough so that the magnetizing current is very low compared to the current we are measuring.
Easy, we use a very high permeability core that has high inductance per turn. Usually some kind of very thin metal foil wound into a toroid shape.
This can be silicon steel, mumetal, or amorphous nanocrystaline material.
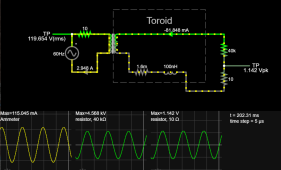
So far so good. It works fine at 50/60Hz, but the very high inductance and large number of turns creates a self resonance at a very few kHz.
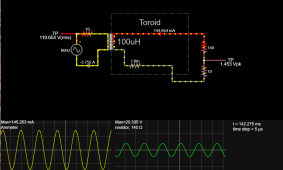
Oh,dear, we want to measure current at 30 kHz, so this will not work. So try again with less turns, and a lower loss core such as very high permeability ferrite. So we use a different core and only 100 turns and we lift the self resonant frequency to 200 Khz. But our 100 turns does not produce much inductance, even with a largish toroid, and our magnetizing current at 30 Khz is going to effect linearity, but we do not care.
We sacrifice some accuracy for something that works at a much higher frequency.
Now if you do the maths, you will find that Faraday's law and the self resonance problem FORCES you to use a high permiability core material with a low loss material, so you need to be a bit choosy about what core you use, and its size.
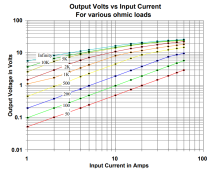
Faraday's law is also very limiting on secondary voltage. If you need a lot of secondary volts, you need a larger core cross section and more turns.
Big difference in designing a CT that will produce 100mV across a burden resistor, and one that will produce 5v across a different burden resistor.
The maths is pretty straightforward, the trick is designing something where all the numbers end up being reasonable. That requires some insight and a few compromises.